If a Graph Has a Hole Is It Continuous

By Ra_Jenna16 10 May, 2022 Post a Comment

We first start with graphs of several continuous functions. But is continuous at.

If There Is A Hole In A Graph Does The Limit Exist Study Com

The first coordinate is certainly.

. The graph of f has a vertical asymptote. Which of the following functions is continuous. The graph of has a hole at.

A continuous function can be represented by a graph without holes or breaks. It is given that f is a continuous function. We now present examples of discontinuous functions.

We could continue the graph in the negative and positive directionsSuch functions are called continuous functions. What are the coordinates of the missing point. The reason is that it equals the function when.

By observing the given graph we come to know that. On what value of x is the function fx C. The graph of f has a jump.

Lim x- x0- f x f x 0 Because we have unfilled circle But lim x- x0 f x f x 0 Because we have the same unfilled circle at the same place Hence the given function is continuous at the point x x 0. A function is continuous if its graph is an unbroken curve. Given that f is continuous in - A graph will have a holejumpbreak only if the function is discontinuous.

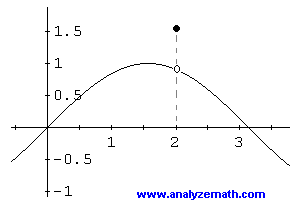
It has a hole or gap. Therefore the original function must have a hole in its graph at. It approaches positive infinity.

Breaks gaps or points at which they are undefined. As your pre-calculus teacher will tell you functions that arent continuous at an x value either have a removable discontinuity a hole in the graph of the function or a nonremovable discontinuity such as a jump or an asymptote in the graph. A function is continuous for example if its graph can be traced with a pen without lifting the pen from the page.

Your pre-calculus teacher will tell you that three things have to be true for a function to be continuous at some value c in its domain. A function whose graph has holes is a discontinuous function. Select all that apply The graph of f has a hole.

That is lim x c f x is a real number The two values are equal. It represents a rational function. Continuity can be defined conceptually in a few different ways.

A graph for a function thats smooth without any holes jumps or asymptotes is called continuous. If either of these do not exist the function will not be continuous at xaxa. This definition can be turned around into the following fact.

Which of the following is TRUE about its graph. The graph of f has a vertical asymptote. A function is continuous.

Any value of x will give us a corresponding value of y. That is lim x c f x f c If a function has a hole the three conditions effectively insist that the hole be filled in with a point to be a continuous function. If f is continuous on what can you say about its graph.

A graph is continuous in the following - Should not break any pointThere are no gaps in the curve. A continuous function is not necessary to have vertical asymptotes. That is the graph has no holes gaps or breaks.

More Definitions Continuity can also be defined on one side of a point using a one-sided limit. A function is continuous at a particular number if three conditions are met. For example if we consider y x 3 which is continuous in - does not contain any vertical asymptotes whereas when we consider y tan x it is continuous.

The functions whose graphs are shown below are said to be continuous since these graphs have no breaks gaps or holes. Select all that apply The graph of f has a hole. Fc must be defined.

Note that this definition is also implicitly assuming that both fafa and limxafxlimxafx exist. It can be drawn without lifting your pen. In fact the simplified function is continuous at.

If the function factors and the bottom term cancels the discontinuity at the x-value for which the denominator was. The graph of f has a jump. This graph is shown below.

Continuous Functions In Calculus